KOI WIN

Восстановление линейных индексных выражений для сведения программ к линейному классу

Д.В. Хмелёв

10 июня 1997 года

Contents

Аннотация

Рассматривается класс нелинейных программ, нелинейность которых вызвана оптимизацией кода программы под последовательную ЭВМ или принципиальными ограничениями используемого процедурного языка. Выделены условия, которые необходимо наложить на текст программы из рассматриваемого класса для того, чтобы можно было свести последнюю к программе линейного класса.

1  Введение

Опыт практической эксплуатации параллельных вычислительных систем показал, что одной из самых сложных проблем стала адаптация программного обеспечения под архитектуру конкретной ЭВМ. Появился целый спектр совершенно новых задач: нахождение потенциального параллелизма, преобразование структур данных под многоуровневую память, нахождение ``узких мест'' и ряд других. Очень часто для решения подобных задач пользуются только исходным текстом программы, проводят его анализ, пытаясь спрогнозировать поведение программы на этапе выполнения и на основании этого знания делают вывод о возможности целевой оптимизации. Проводимый анализ часто называют статическим анализом, поскольку никакой информации со стадии исполнения программы не используется.

Важным источником адаптируемых программных систем является огромный арсенал программного кода, накопленный за полвека использования последовательных ЭВМ. Одним из основных достоинств этих программ является их надежность, проверенная десятилетиями эксплуатации. К сожалению, попытки ускорить исполнение программы на суперкомьютере иногда наталкиваются на трудности, связанные с тем, что программный код оптимизирован под последовательную ЭВМ.

subroutine S1(P,N)	subroutine S2(P,N)	subroutine S3(P,N)
dimension P(1)	dimension P(1)	dimension P(1)
		dimension P17(N,N)
		С Expanding P to P17
		ii = 1
		do i = 1, N
		do j = 1, i
		P17(j,i) = P(ii)
		ii=ii+1
		end do
		end do
ii = 1	C     ii = 1	С Source text with P17
do i = 1, N	do i = 1, N	do i = 1, N
do j = 1, i	do j = 1, i	do j = 1, i
P(ii) = 1/(i+j-1)	P(j+(i-1)*i/2) = 1/(i+j-1)	P17(j,i) = 1/(i+j-1)
ii=ii+1	C     ii=ii+1	C     ii=ii+1
end do	end do	end do
end do	end do	end do
		С Packing P17 to P
		ii = 1
		do i = 1, N
		do j = 1, i
		P(ii) = P17(j,i)
		ii=ii+1
		end do
		end do
return	return	return
end	end	end

Рис. 1:

Рассмотрим следующую ситуацию: для вычислительной задачи был составлен алгоритм, в котором существенную роль играют действия с двух- и более мерными массивами; при программной реализации алгоритма, чтобы получить более эффективный код, многомерные массивы были вытянуты в векторы; при этом выражения для индексов массивов усложнились и стали, вообще говоря, нелинейно зависеть от параметров циклов и внешних (по отношению к данному фрагменту программы) переменных. Для того, чтобы при вычислении индексных выражений не использовать операции умножения, вводят индуктивные переменные, которые изменяются в циклической конструкции только посредством прибавлений константы и присваиваний таким образом, чтобы на соответствующей итерации они совпадали с нужным индексным выражением.

Другая ситуация связана с использованием структуры данных, которая формально не присутствует в языке, например треугольной матрицы или многомерного массива, координатные размерности которого зависят от внешних переменных. В этом случае многомерные массивы также вытягиваются в векторы и происходит преобразование программы, аналогичное только что изложенному.

В результате программа теряет читаемость и те возможности для ускорения, которые присутствовали в исходном алгоритме. Примером такой программы может послужить подпрограмма S1, изображенная на рисунке 1. Мы видим, что индексное выражение массива P равно индуктивной переменной ii, значение которой каким-то образом зависит от параметров цикла. В большинстве случаев (и, в частности, здесь) можно предъявить индексную функцию, которая выражает значение переменной ii на конкретной итерации цикла через параметры объемлющих циклов и внешние по отношению к данному фрагменту программы переменные. В данном случае ii = i(i-1)/2+j. Поиск индексной функции в общем случае представляет отдельную сложную проблему, которая не будет затронута в рамках данной работы. В дальнейшем будем считать, что при исследовании текста программы каким-то образом удалось найти индексные функции и, подставив их вместо индексных переменных, получить, вообще говоря, нелинейное индексное выражение, зависящее только от параметров объемлющих циклов и внешних переменных. Проделав такую операцию над подпрограммой S1, получаем подпрограмму S2.

Мы рассматриваем программу из класса, которому, в частности, принадлежит S2. Нам недоступно описание исходного алгоритма, который она реализует. Наши возможности ограничиваются только формальным анализом текста программы. Логично предположить, что мы оказались именно в той ситуации, которую описали выше и нелинейность индексных выражений вызвана вытягиванием многомерного массива в вектор. Наша задача состоит в том, чтобы восстановить исходную ``естественную'' запись программы.

В этой статье исследуются условия, при выполнении которых последняя проблема разрешима в случае, когда ``упаковывается'' треугольная матрица. Мы найдем некоторые естественные достаточные условия того, что линейные индексные выражения могут быть восстановлены исходя только из нелинейного индексного выражения. Оказывается, в общем случае возможно бесконечное число таких восстановлений. Для выделения из этих многих вариантов ``настоящего'' требуется использовать информацию о структуре объемлющих циклов. Будут найдены достаточные условия конечности числа вариантов восстановления. Самым удивительным результатом работы является теорема 7, которая говорит, что если индексное выражение зависит только от параметров циклов и в пространстве итераций существует вершина, положение которой не зависит от внешних параметров, то существует не более одного варианта восстановления линейных индексных выражений. Например, подпрограмма S2 удовлетворяет условию этой теоремы.

Пользуясь техникой, изложенной в статье, можно найти этот единственный пригодный вариант восстановленных линейных индексных выражений в подпрограмме S2. Проиллюстрируем теперь способ представления исходной записи алгоритма. Преобразуем массив P в полноразмерный массив P17, который состоит из нижнего треугольника с диагональю, содержащего элементы P, и верхнего треугольника без диагонали, содержащего неиспользуемые элементы. Таким образом, получаем процедуру S3, которая эквивалентна исходной в смысле результатов работы. Индексные выражения второго гнезда циклов, который выполняет вычисления, а, следовательно, наиболее интересен, принимают стандартную линейную форму. Появляется наглядность: становится ясно, что подпрограмма S3 заполняет упакованный треугольный массив P элементами известной матрицы Гильберта порядка N.

Единственный неприятный момент состоит в том, что подпрограмма S3 запрашивает в три раза больше памяти, чем необходимо: вводится новый массив удвоенного размера, но остается и старый. Это результат чересчур прямолинейного восстановления естественной формы записи исходного алгоритма. Если, например, расширить семантику языка Фортран и ввести новый тип ``треугольный массив'', то вообще никакой дополнительной памяти не потребуется (но зато потребуется изменить компилятор). Проблему памяти можно решать другими методами: самое главное, что фрагмент программы приобрел естественный вид и возможен адекватный статический анализ этого фрагмента.

Данная работа примыкает к задаче отображения проблем вычислительной математики на архитектуру вычислительных систем, которая рассматривалась в книгах [1] и [2]. Проблематика статьи возникла из желания расширить класс программ, для которых возможен эффективный статический анализ.

2  Модель входного фрагмента программы

В п. 2.1 формально определен линейный класс программ и множество фрагментов, которые мы будем исследовать. П. 2.2 посвящен полному описанию той информации о фрагменте, которую можно получить пользуясь только текстом программы. П. 2.3 посвящен описанию используемого математического аппарата и доказательству важной технической леммы. Далее всюду используются стандартные обозначения: Z - кольцо целых чисел, R - поле действительных чисел.

2.1   Основные определения

Наиболее распространенным языком программирования для суперЭВМ является Фортран. Согласно установившейся традиции, мы будем изучать фрагменты программ на языке Фортран, хотя все полученные результаты, с несущественными изменениями формулировок, применимы к любому процедурному языку.

Будем говорить, что выражение, содержащееся в операторе S фрагмента, имеет стандартную линейную форму, если оно имеет вид: f₁ x₁+╪+ f_n x_n+f₀+f_n+1 z₁+╪+f_n+p z_p, где x₁, ..., x_n - параметры объемлющих оператор S циклов, предположим, что их имеется ровно n; f₀, ..., f_n+p н Z; z₁, ..., z_p - целочисленные переменные, не изменяемые в данном фрагменте (такие переменные будем называть внешними для данного фрагмента), предположим, что их имеется ровно p. Все операторы, осуществляющие выбор последующего действия в зависимости от истинности некоторого условия, будем называть альтернативными операторами. Тело цикла при каком-то одном значении управляющего параметра назовем итерацией цикла (например, заголовок ``DO 1 i=1,N'' задает N итераций). Будем предполагать, что проверка значения управляющего параметра происходит перед выполнением итерации (так, как принято в Фортране-77).

Определение 1. Фрагмент программы принадлежит линейному классу при выполнении следующих условий:

1) он состоит только из операторов присваивания, операторов цикла DO, альтернативных операторов (IF и пр.) и операторов безусловного перехода, причем все циклы фрагмента заданы только операторами DO;

2) все индексные выражения всех обращений к массивам, условия альтернативных операторов, начальные и конечные значения параметров всех циклов имеют стандартную линейную форму;

3) шаг изменения параметров DO-циклов равен единице. Линейный класс программ занимает среди программного обеспечения примерно такое же место, как матрицы в конечномерном анализе, линейные дифференциальные уравнения в теории обыкновенных дифференциальных уравнений, численные методы линейной алгебры в вычислительной математике и т.п. В [1] показано, как для конкретного фрагмента, принадлежащего линейному классу, можно эффективно построить исчерпывающее описание его графа алгоритма с помощью системы функций, линейных как по параметрам цикла, так и по внешним переменным. В [3] доказан фундаментальный факт: для любой программы линейного класса набор таких функций конечен и не зависит от значений внешних переменных.

Будем рассматривать проблему преобразования к линейному классу фрагментов, для которых частично не выполнено условие 2. Этот класс будем называть Virtual Dimension или, сокращенно, VD.

Определение 2. Фрагмент программы принадлежит классу VD, если он удовлетворяет условиям 1), 3), и 2), за тем исключением, что индексные выражения некоторых обращений к массивам имеют вид многочлена от параметров объемлющих циклов и внешних переменных.

Не приходится рассчитывать, что любая программа имеет вид, который требуется в последнем определении, но подавляющее большинство программ можно привести к нужному виду, причем привести, разумеется, с гарантией сохранения результатов вычислений. За более подробной информацией читатель может обратиться к статье [4].

2.2  Модель адресного обращения

Рассмотрим фрагмент программы класса VD. Множество W векторов z = (z₁, ..., z_p)^T будем называть пространством внешних переменных. Будем считать, что W задается набором линейных неравенств.

Поскольку различие линейным и VD классами состоит только в форме обращений к массивам, нас прежде всего должна интересовать структура конкретного обращения к массиву. Рассмотрим оператор S нашего фрагмента, в котором находится обращение O к массиву, название которого обозначим через P. Вследствие определения фрагментов класса VD, при фиксированном z множество всех допустимых комбинаций параметров циклов x = (x₁, ╪, x_n)^T принимает значения из многогранника W^I(z), который будем называть пространством итераций. Из определения класса VD вытекает, что многогранник W^I(z) описывается с помощью параметризованной системы линейных неравенств Ax ё b(z), где каждая компонента b(z) имеет стандартную линейную форму. Будем говорить, что выражение для индекса массива P по k-той координате имеет стандартную полиномиальную форму, если оно записывается в виде многочлена g(x,z) многих переменных над полем рациональных чисел. Предположим, что для любого z н W множество W^I(z) непусто и ограничено.

Определение 3. Будем называть адресным обращением набор

Л М Н \mathstrut S, O, P, k, z, W, x, A, b(z), g(x,z) Э Щ Ч

(2.1)

удовлетворяющий приведенным выше условиям. Например, в подпрограмме S2 адресное обращение единственно и его компоненты определяются следующим образом:

S, O, P = ``P╒╒, k = 1,z = (N),W = {N | N Ё 1},       x = Ф Г Г Г Х i j Ж В В В Ь ,b = Ф Г Г Г Г Х -1 N -1 0 Ж В В В В Ь ,A = Ф Г Г Г Г Х -1 0 1 0 0 -1 -1 1 Ж В В В В Ь , g(x,z) = x1(x1-1) 2 +x2.

2.3  Параметрическое линейное программирование

Восстановленные линейные индексы многомерного массива обязаны удовлетворять некоторым линейным неравенствам, которые должны быть выполнены при всех допустимых комбинациях параметров объемлющих циклов. Для проверки неравенств необходимо находить минимум линейного функционала на пространстве итераций, которое зависит от внешних переменных. В этом пункте мы развиваем математический аппарат, необходимый для решения этой задачи.

Построим алгоритм нахождения параметрического минимума стандартной линейной формы f₁ x₁+╪+ f_n x_n+f₀+f_n+1 z₁+╪+f_n+p z_p = (f_x,x)+(f_z,z)+f₀, где (·,·) обозначает скалярное произведение в пространствах одинаковой размерности, f_x = (f₁,╪,f_n)^T, f_z = (f_n+1,╪,f_n+p)^T, индекс T обозначает транспонирование:

min Ax ё b(z)  [(fx,x)+(fz,z)+f0] = (fz,z)+f0+ min Ax ё b(z)  (fx,x).

Обозначим c = f_x. Выше мы потребовали, чтобы множество W задавалось набором линейных неравенств. Поэтому если подразумевается z н Z^p (соответственно, z н R^p), то под множеством W мы понимаем все целочисленные (соответственно, все действительные) решения этих неравенств. Рассмотрим следующую задачу параметрического линейного программирования на линейном пространстве L = Z, R:

PL(z, W): min Ax ё b(z)  (c,x) ,где A = (aij)m ×n н Zm ×n,z н W л Lp,c н Zn, x н Ln,       b(z) = (b1(z),╪,bm(z))T,bi(z) = (bi,z)+bi0, bi н Zp,bi0 н Z для i = 1,m   .

(2.2)

Мы считаем, что множество W обладает свойством "z н W допустимое множество M(A,b(z)) = {x н Lⁿ | Ax ё b(z)} непусто и ограничено: это является вполне естественным условием конечности времени исполнения и нетривиальности фрагмента программы. Для выделения множества W исходя из системы неравенств Ax ё b(z) в случае L = R можно воспользоваться методом Фурье-Моцкина, описанным в [5]. Если пространство L целое ( L = Z), матрица A и вектор-функция b(z) совпадают с матрицей и вектор-функцией адресного обращения (2.1), то M(A,b(z)) совпадает с W^I(z): M(A,b(z)) = W^I(z).

Вектор x^*(z) является решением, если при фиксированном z для любых допустимых x (c,x^*(z)) ё (c,x). Значением задачи PL называется функция f(z) = (c,x^*(z)).

Рассмотрим двойственную к (2.2) задачу линейного программирования

DL(z,W)\mathrel: max ATy = c;  y ё 0  (b(z),y) , где y н Lm.

(2.3)

Вектор y^*(z) является решением, если при фиксированном z для любых допустимых y: (b(z),y^*(z)) Ё (b(z),y). Значением задачи DL(z,W) называется функция (b(z),y^*(z)).

Из непустоты и ограниченности M(A,b(z)), следует, что значение DR(z,W) существует и совпадает со значением PR(z,W) (см. [6]). Многогранник ограничений задачи DR(z,W) также непуст и ограничен, а, следовательно, имеет конечное число w вершин y¹, ..., y^w. Поскольку значение задачи DR(z,W) совпадает со значением функционала (b(z),y) в некоторой вершине допустимого множества задачи DR(z,W), справедлива формула:

f(z) = max k = [`1,w]  (b(z),yk).

(2.4)

Лемма 1 Для полиэдра W л R^p такого, что "z н W допустимое множество M(A,b(z)) непусто и ограничено, существует конечное, не зависящее от значений внешних переменных, разбиение на полиэдры, такое что на каждом из них координаты вершин M(A,b(z)) являются линейными формами с рациональными коэффициентами от z.

Доказательство Наше доказательство состоит в построении нужного разбиения. Введем необходимые обозначения. Пусть задано множество v л {1, ..., m}. Упорядочим элементы v по возрастанию: v = {v₁ < v₂ < ╪ < v_k}. Для произвольного вектора a мы понимаем под a_v вектор из k компонент, имеющий следующий вид: a_v = (a_v1, a_v2, ..., a_vk)^T. Обозначим через A_v матрицу из строк v₁, ..., v_k матрицы A. Рассмотрим задачи параметрического линейного программирования для c = -(A_{i})^T.

PRi(z,W): min Ax ё b(z)  (c,x).

Двойственная задача имеет вид

DRi(z,W): max ATy = c; y ё 0  (b(z),y).

Базисом называется всякая невырожденная матрица, составленная из n строк матрицы A. Пусть номера строк задаются множеством v. Допустимым базисом задачи DR_i называется такая матрица B = A_v, что (B^T)^-1c ё 0. Рассмотрим точку x(z) = B^-1b_v(z). Обозначим [`v] = {1, ..., m}\v, N = A<sub>[`v]</sub>. Ввиду [7] точка x(z) является вершиной допустимого множества задачи PR_i тогда и только тогда, когда выполнена система неравенств Nx(z) ё b_{[`v]</sub>(z) или A<sub>[`v]}(A_v)^-1b_v(z) ё b_[`v](z). Последняя система определяет полиэдр в пространстве внешних переменных, для которого координаты вершины x(z) линейно зависят от z. Перебрав все допустимые базисы для задачи DR_i и решив соответствующие системы, мы найдем, вообще говоря, неоднородные кусочно-линейные не всюду определенные функции, которые задают координаты вершин полиэдра M(A,b(z)). Эти вершины лежат на грани M(A,b(z)), которая лежит в плоскости (c,x) = -b_i(z) (или A_{i}x = b_i(z)); число кусков линейности каждой координатной функции конечно. Носитель каждой функции является объединением конечного числа полиэдров.

Аналогичное построение верно для i = [`1,m]. Утверждение леммы вытекает из конечности числа носителей функций и конечности числа вершин. q.e.d.

Значение ``непрерывной'' задачи PR(b(z), W) при целом z всегда меньше либо равно значения ``целой'' задачи PZ(b(z), W). Они совпадают, если многогранник ограничений Ax ё b(z) является целочисленным, то есть все его вершины при целых z имеют только целочисленные координаты. Такие полиэдры возникли в связи с так называемой ``транспортной задачей''. Еще основателями теории линейного программирования, был описан класс таких матриц A, что многогранник ограничений M(A,b) является целочисленным при любом целом b.

Заметим, что наш класс матриц включается в этот. Действительно, вектор b(z) при целочисленном z является целочисленным, но зависит не от m параметров, а от p, причем совсем не обязательно p = m. На практике p << m, чаще всего p = 1, реже p = 2. Поэтому теоремы, рассмотренные ниже, дают достаточные условия на целочисленность M(A,b(z)).

Определение 4. Назовем целочисленную матрицу A абсолютно унимодулярной, если все ее миноры равны либо 0, либо ╠1.

Теорема 1 Множество M(A,b) целочисленно при любом целочисленном векторе b тогда и только тогда, когда матрица A абсолютно унимодулярна.

Эта теорема доказана в [8], но более фундаментальное рассмотрение - в [9]. ограничений. При больших m и n проверка унимодулярности может занять много времени, поэтому сформулированы достаточные признаки унимодулярности.

Теорема 2 Пусть A - целочисленная матрица из {╠1, 0} с не более чем двумя ненулевыми элементами в каждом столбце. Для того чтобы A была абсолютно унимодулярной, необходимо и достаточно, чтобы строки е\" можно было разбить на два класса, обладающих следующими свойствами.

1) Если строки i и k принадлежат одному и тому же классу и для некоторого j имеем a_ij ╧ 0, a_kj ╧ 0, то a_ij = -a_kj.

2) Если строки i и k принадлежат разным классам, и для некоторого j имеем a_ij ╧ 0, a_kj ╧ 0, то a_ij = a_kj.

Доказательство теоремы и алгоритм проверки достаточного условия на унимодулярность приведены в [10]. См. также [11]. Практика показывает, что исключительно много адресных обращений в реальных программах обладают абсолютно унимодулярной матрицей.

3  Восстановление треугольных массивов

3.1  О хранении элементов массивов в памяти

Пусть требуется хранить все элементы квадратной матрицы T(I,J), I,J = [`1,q] в последовательных ячейках памяти. Самым естественным (и наиболее часто используемым) способом распределения памяти является такой способ, при котором матрица располагается в памяти в лексикографическом порядке индексов или, как иногда говорят, ``по строкам'':

T(1,1), T(1,2), ╪, T(1,q), T(2,1),╪,T(q,q-1), T(q,q).

(3.1)

Например, именно так организовано хранение матриц в языке Си. В языке Фортран используется метод, при котором матрица располагается в памяти в антилексикографическом порядке индексов. Пара индексов (I,J) антилексикографически старше пары индексов (I╒,J╒), если J > J╒. В случае J = J╒, пара (I,J) старше пары (I╒,J╒), если I > I╒. При таком способе матрица T(I,J) хранится следующим образом:

T(1,1), T(2,1), ╪, T(q,1), T(1,2),╪,T(q-1,q), T(q,q).

(3.2)

Обозначим через LOC_lex(T(I,J)) адрес в памяти элемента T(I,J), хранящегося способом (3.1), а через LOC_antilex(T(I,J)), соответственно, способом (3.2). Для произвольных K, L = [`1,q]

LOClex(T(K,L)) = LOCantilex(T(L,K)).

В дальнейшем будем считать, что массивы хранятся в памяти лексикографическом порядке индексов, но, записывая обращение к элементу массива языка Фортран, будем заменять порядок индексов на обратный. Именно поэтому мы переставили индексы i и j в обращении к массиву P17 в программе S3 на рисунке1. Смысл этой операции состоит в том, что сохраняется линейная упорядоченность в памяти элементов упакованного массива, которые составляли, в случае c S2 и S3, столбец восстановленного массива. За более подробной информацией можно обратиться к книге [12].

3.2  Варианты хранения треугольного массива

Пусть элементы массива T(J,I) определены не для всех индексов, а только для одного из следующих множеств:

A1 = Л М Н (I,J) | I = \mathstrut 1,q   ,J = \mathstrut 1,I   Э Щ Ч , A2 = Л М Н (I,J) | I = \mathstrut 1,q   ,J = \mathstrut 1, q-I+1   Э Щ Ч , A3 = Л М Н (I,J) | I = \mathstrut 1,q   ,J = \mathstrut q-I+1,q   Э Щ Ч , A4 = Л М Н (I,J) | I = \mathstrut 1,q   ,J = \mathstrut I,q   Э Щ Ч .

В каждом из приведенных множеств q(q+1)/2 пар. Предположим, что элементы из T хранятся в одномерном массиве T╒(1:q(q+1)/2) в лексикографическом порядке индексов. Индекс элемента T(J,I) в массиве T╒ определяется с помощью специальных функций, представленных в таблице.

Таблица

множество индексов соответствующая функция A1, F(I,J) = I(I-1)/2+J, A2, G(I,J) = -I(I-1)/2+q(I-1)+J, A3, F╒(I,J) = F(I,J-(q-I)+1), A4, G╒(I,J) = G(I,J-I+1).

Рассмотрим адресное обращение (2.1) к массиву T╒(1:q(q+1)/2). Предположим, что индексные выражения L(x,z) и R(x,z) массива T имели стандартную линейную форму, то есть, на итерации x циклической конструкции производилось обращение к элементу T(R(x,z),L(x,z)). Пара индексных выражений (L(x,z),R(x,z)) принадлежит множеству индексов A_t, где t н {1,2,3,4}. На итерации x обращение к элементу массива T╒, соответствующему T(R(x,z),L(x,z)), можно записать в виде функции от R(x,z) и L(x,z), соответствующей множеству A_t. Из текста программы известна функция g(x,z), которая получается после подстановки линейных индексных выражений в специальную функцию. Если, например, t = 3, то g(x,z) = F╒(L(x,z),R(x,z)).

Наша общая задача восстановления линейных индексных выражений в данном случае состоит в том, чтобы выделить множества W_k л W, на которых можно задать стандартные линейные формы L_k(x,z) и R_k(x,z), удовлетворяющие следующим условиям

а) (L_k(x,z),R_k(x,z)) н A_t для любого x н M(A,b(z)),

б) функция, соответствующая A_t, от L_k(x,z) и R_k(x,z) равна g(x,z).

Поскольку мы хотим найти представление g(x,z) в виде композиции специального многочлена второй степени и стандартных линейных форм L и R, то сразу возникает необходимое ограничение на степень g: она не должна превосходить 2.

Посредством линейных замен пары из A₃ и A₄ переводятся в пары из A₁ и A₂ соответственно. Поэтому для g(x,z) должно быть справедливо одно из представлений:

╥ g(x,z) = F(L(x,z), R(x,z)),  Ф Х L(x,z), R(x,z) Ж Ь н A1, ╥ g(x,z) = G(L(x,z), R(x,z)),  Ф Х L(x,z), R(x,z) Ж Ь н A2.

Классификация. Знак коэффициента при квадрате любой переменной вектора x в многочлене g(x,z) является инвариантом, однозначно определяющим выбор представления:

1) если коэффициент положителен, то g = F(·,·),

2) если коэффициент отрицателен, то g = G(·,·).

Если у квадратов разных переменных x различны знаки, то восстановить линейные индексные выражения нельзя. Если квадраты переменных x отсутствуют, то возможны два случая.

Случай 1. g(x,z) является линейной неоднородной функцией x - тогда выбор представления следует согласовывать с другими обращениями к этому массиву; при этом возможны два варианта:

a) g(x,z) = F(a(z),R(x,z)), 1 ё R(x,z) ё a(z), или g(x,z) = G(a(z),R(x,z)), 1 ё R(x,z) ё q-a(z)+1, здесь L(x,z) равно линейной неоднородной функции a(z), это означает, что программа обращается непосредственно к строке a(z) треугольной матрицы;

б) не существует такой константы a, чтобы было выполнено одно из условий предыдущего пункта, это означает, что массив проходится нерегулярно - циклическая конструкция не согласована со структурой многомерного массива; можно попытаться согласовать данное адресное обращение с другими к этому же массиву при помощи расщепления циклов.

Случай 2. В противном случае нельзя представить g(x,z) в виде композиции одной из функций F или G и линейных форм (таким образом, адресные обращения вроде T(I*J)) исключены).

Рассмотрим технику восстановления линейных индексных выражений для адресного обращения с функцией F. Аналогичную технику можно применить для случая с G.

3.3   Основное разложение индексной функции

Найдем разложение функции g(x,z) в предположении, что коэффициент при квадрате любой переменной g(x,z) больше нуля (это соответствует представлению g(x,z) = F(L(x,z), R(x,z))). Введем обозначение y^T = (x^T,z^T).

Определение 5.Назовем функцию

Q[y] = n+p Е i = 1  n+p Е j = 1  qij yiyj

квадратичной формой от вектора y н R^n+p.

Лемма 2 Квадратичная форма Q[y] ╧ 0 разлагается в квадрат линейного функционала от y тогда и только тогда, когда она симметрична с неотрицательными элементами на диагонали и каждые два ненулевых столбца матрицы Q пропорциональны.

Будем у произвольной функции f(x,z) опускать аргументы x и z, если речь идет об ее символьной записи. В этом случае под операциями сложения и вычитания, умножения, подстановки следует понимать соответствующие операции с символьными записями с приведением подобных членов. Если g = F(L,R), L и R имеют стандартную линейную форму, то справедливо разложение 2g(x,z) = Q[y]+f(y), где Q[y] удовлетворяет условиям леммы, а f(y) - линейная форма. Пусть Q[y] = ([L\tilde](y))². Линейную форму L(y) можно определить с точностью до знака и константы: L(y) = ╠[L\tilde](y)+const. Поэтому если коэффициенты линейной формы [L\tilde](y) не целые, то восстановить линейные индексные выражения нельзя.

Вычислим символьно:

~ R   = g- ~ L   ( ~ L   -1)/2.

Если у линейной формы [R\tilde] существует нецелый коэффициент, то восстановить линейные индексные выражения нельзя. В дальнейшем будем предполагать, что [L\tilde](x,y) и [R\tilde](x,y) имеют стандартную линейную форму.

do i=p,p+q

do j=r,r+s

A(j+i*(i-1)/2)=i+j

enddo

enddo

Рис. 2:

3.4  Эвристические соображения

Существует ли фрагмент программы класса VD, который имеет бесконечно много вариантов восстановления линейных индексных выражений (для различных внешних параметров)? Как ни странно, такой фрагмент действительно существует. Его код приведен на рисунке 2.

Исследуем этот фрагмент в предположении, что нам заведомо ничего не известно про параметры p, q, r и s. В первую очередь заметим, что для адресации используется специальная функция F(·,·). С помощью пункта 3.3 выделяем L₀ = [L\tilde] = i, R₀ = [R\tilde] = j. На первый взгляд, в программе обрабатывается прямоугольник размера (q+1)×(s+1). Тем более удивительно, что это не единственный вариант обработки упакованного треугольного массива. Зададим

Lk = Lk-1+1 = i+k; Rk = Rk-1-Lk-1 = j-ki-k(k-1)/2, k н Z.

Из вида F вытекает F(L₀,R₀) = F(L_k,R_k). Программа, изображенная на рисунке 2, обрабатывает фрагмент треугольного массива тогда и только тогда, когда для всех точек пространства итераций выполнено: L_k(i,j) Ё 1, R_k(i,j) Ё 1, [L_k(i,j) Ё R_k(i,j) ш(L_k-R_k)(i,j) Ё 0]. Составим систему неравенств на внешние параметры: для i = [`(p,p+q)], j = [`(r,r+s)],

Л О М О Н Lk(i,j) Ё 1, Rk(i,j) Ё 1, (Lk-Rk)(i,j) Ё 0 ш Л О М О Н p+k Ё 1, r-k(p+q)-k(k-1)/2 Ё 1, -(r+s)+(k+1)p+k(k+1)/2 Ё 0.

Найдем нетривиальное решение последней системы.

k = t, q = t, s = t, p = 1+t2, r = t3+t2+t(t+1)/2+1, где t = 1, 2, ╪ .

При такой параметризации

r-k(p+q)-k(k-1)/2 = t3+t2+t(t+1)/2+1-t(1+t2)-t2-t(t-1)/2 = 1, -(r+s)+(k+1)p+k(k+1)/2 = -(t3+t2+t(t+1)/2+1)-t       +(1+t)(1+t2)+ t(t+1) 2 = 0

и требуемые неравенства выполняются. Следовательно, требуемый пример построен и в классе VD существуют программы, которые могут иметь бесконечно много вариантов восстановления линейных индексных выражений. В нашем примере такими выражениями являются L_t и R_t для t = 1, 2, ╪.

Может показаться, что пример довольно сомнителен: в реальной программе значения p, q, r и s определены заранее и к началу исполнения фрагмента они известны, а следовательно, такого изобилия вариантов может и не быть. Поэтому еще раз подчеркнем, что мы рассматриваем фрагмент отдельно от всей программы и про p, q, r и s заведомо ничего не известно. Такая постановка задачи вполне соответствует духу статического анализа: определить структуру фрагмента, и лишь затем согласовывать ее с остальными структурами. Разобранный пример демонстрирует, что множество программ, которые можно задать с помощью процедурного языка, значительно шире множества реальных программ. Редкий разработчик программного обеспечения закладывает в текст программы бесконечно большое количество вариантов ее поведения в зависимости от значений внешних параметров. Поэтому на практике такое разнообразие не встречается, а, следовательно, встает задача выделения класса таких фрагментов, для которых существует лишь конечное число вариантов их восстановления. Теоремы следующего пункта дают возможность выделить такой класс.

3.5  Теоремы восстановления

Рассмотрим адресное обращение (2.1). Предположим, что, воспользовавшись техникой пункта 3.3, нам удалось выделить стандартные линейные формы L₀ и R₀, такие, что F(L₀,R₀) = g (вообще говоря, L₀ известно с точностью до знака; предположим, что знак фиксирован). Исходное индексное выражение L отличается от L₀ на некоторую неизвестную константу. Обозначим L_k = L₀+k. Линейная форма R_k определяется из условия F(L_k,R_k) = g. Поэтому все возможные пары (L_k,R_k) задаются равенствами L_k = L₀+k, R_k = R₀-kL₀-k(k-1)/2.

Лемма 3 Для фиксированного z н W стандартные линейные формы L_k(x,z) и R_k(x,z) являются корректными индексными выражениями в треугольном массиве тогда и только тогда, когда

"x н M(A,b(z)): 1 ё Rk(x,z) ё Lk(x,z).

(3.3)

Для стандартных линейных форм L₀(x,z) и R₀(x,z) справедливо представление L₀(x,z) = (x_x,x)+(x_z,z)+l₀, R₀(x,z) = (c_x,x)+(c_z,z)+r₀, где x_x, c_x н Zⁿ; x_z, c_z н Z^p; l₀, r₀ н Z. Пользуясь теоремами пункта 2.3, обнаруживаем, что можно найти параметрический минимум функций L₀(x,z) и R₀(x,z) на полиэдре M(A,b(z)). Условимся обозначать минимум стандартной линейной формы f(x,z) на многограннике M(A,b(z)) с помощью верхнего индекса:

fmin(z) = min x н {Ax ё b(z) }  f(x,z).

Предположим, что f^min(z) всегда имеет стандартную линейную форму при z н W. Это условие не ограничивает общности, так как в противном случае согласно (2.4) и лемме 1 можно разделить W на части, на каждой из которых f^min(z) будет линейной формой.

Рис. 3:

Лемма 4 Для фиксированного z н W условие (3.3) выполнено тогда и только тогда, когда

1 ё Rkmin(z) и (Lk-Rk)min(z) Ё 0.

(3.4)

Зададим плоскость LR с осью ординат L и осью абсцисс R. Предположим, что "z н W координаты v вершин M(A,b(z)) являются линейными формами от z: xⁱ(z) = (Bⁱ(z)+bⁱ₀), где Bⁱ:R^p╝Rⁿ линейный оператор, bⁱ₀ н Rⁿ. Из леммы 1 следует, что это условие не ограничивает общности. Сопоставим точке z н W точку Xⁱ(z) на плоскости LR с координатами

Xi(z) = Ф Г Х L0(xi(z),z) R0(xi(z), z) Ж В Ь .

Xⁱ отображает выпуклое множество внешних параметров W в выпуклое множество (возможно, вырожденное в луч, отрезок или точку) [(W)\tilde] на плоскости LR. Определим на плоскости LR множества M_k = {(L,R)^T: 1 ё R-kL-k(k-1)/2 ё L+k }. На рисунке 3 изображены области M_k для k = [`(-2,4)]: угол множества M₄ находится в точке (-3,-5)^T, угол множества M_-2 в точке (3,-2)^T. Свойства множеств M_k перечислены в следующей лемме.

Лемма 5 Справедливы следующие утверждения.

1) M_k ограничиваются прямыми R_k(L) = kL+k(k-1)/2 и R_k+1(L) = (k+1)L+k(k+1)/2: M_k = {R_k(L) Ё 1}г{R_k+1(L) ё 0}.

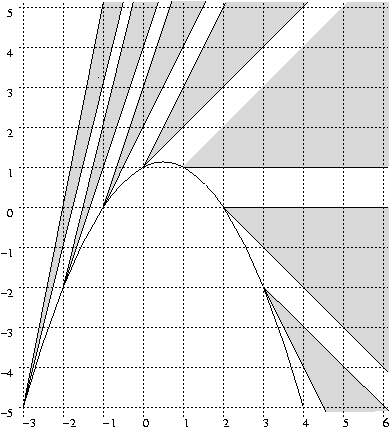
2) Каждое M_k ограничивается углом, вершина которого лежит на параболе P(L) = 1-L(L-1)/2 и имеет координаты (1-k,1-k(k-1)/2)^T.

3) Для любых j ╧ k множества M_j и M_k не пересекаются.

4) Рассмотрим ограниченное множество M на плоскости LR. Множество M пересекается лишь с конечным числом M_k или не пересекается ни с одним из M_k.

5) Зададим в плоскости LR множество U с помощью прямых U₁(L) = U₁₁L+U₁₂ и U₂(L) = U₂₁L+U₂₂, U₁₁ > U₂₁: U = {(L,R)^T: R ё U₁₁L+U₁₂, R Ё U₂₁L+U₂₂ }. Множество U пересекается лишь с конечным числом M_k.

Поскольку L_k-R_k = -R_k+1, условие (3.4) можно записать в виде: 1 ё R_k^min(z) и (-R_k+1)^min(z) Ё 0. Введем обозначение W_k = Wг{z:1 ё R_k^min(z)}г{z:(-R_k+1)^min(z) Ё 0}.

Лемма 6 Точка z н W_k тогда и только тогда, когда для всех вершин i = [`1,v] полиэдра M(A,b(z)) выполнено Xⁱ(z) н M_k.

Доказательство Подставим в неравенства, задающие M_k, координаты Xⁱ(z) (i = [`1,v]): 1 ё R₀(xⁱ(z),z)-kL₀(xⁱ(z),z)-k(k-1)/2 ё L₀(xⁱ(z),z)+k. Утверждение леммы следует из леммы 3 и известного факта из теории линейного программирования: экстремальное значение линейного функционала на полиэдре M(A,b(z)) достигается в некоторой вершине. q.e.d.

Лемма 7 Для любых целых чисел j и k таких, что j ╧ k, W_jгW_k = ф.

Доказательство Предположим, что $z н W_j:z н W_k. Тогда для всех вершин i = [`1,v] полиэдра M(A,b(z)) выполнено Xⁱ(z) н M_j и Xⁱ(z) н M_k. Но множества M_j и M_k не пересекаются ввиду утверждения 3) леммы 5. q.e.d.

Пользуясь алгоритмами параметрического линейного программирования пункта 2.3, можно разбить W на непересекающиеся многогранники W_k так, что z н W_k тогда и только тогда, когда для z и k выполнено (3.3). Для z н W_k искомыми индексными выражениями являются L_k и R_k. Адресное обращение (2.1) имеет конечное число вариантов восстановления линейных индексных выражений тогда и только тогда, когда лишь конечное число множеств W_k целочисленно не пусты. Достаточным признаком целочисленной непустоты W_k является непустота W_k. Следующие теоремы дают достаточные признаки непустоты лишь конечного числа W_k. Все эти теоремы имеют силу для адресных обращений с матрицей A, которая не является абсолютно унимодулярной. Унимодулярность A требуется только при реализации алгоритма, описанного в пункте 2.3.

Теорема 3 Если множество W внешних параметров ограничено, то не более чем конечное число множеств W_k непусто.

Доказательство Для произвольной вершины многогранника M(A,b(z)) множество [(W)\tilde] = Xⁱ(W) является ограниченным. Утверждение теоремы следует из леммы 6 и пункта 4) леммы 5. q.e.d.

Определение 6.Назовем лучом L_{z0, v} множество L_{z0, v} = {z н R^p:z = z₀+av,a Ё 0}. Будем называть точку z₀ основанием луча, а вектор v - направлением луча. Из каждого основания луч может выходить по нескольким направлениям. Будем обозначать через V(z₀) множество направлений всех лучей, которые выходят из основания z₀.

Лемма 8 Произвольный неограниченный полиэдр можно представить в виде объединения лучей так, что множество W^z оснований лучей ограничено, а каждое направление луча из множества V(z₀) имеет единичную норму:

W = х z0, v   Lz0,v, z0 н Wz: ||z0|| < b, v н V(z0), ||v|| = 1 .

(3.5)

Эта лемма следует из [7].

Теорема 4 Пусть существует такая вершина i полиэдра M(A,b(z)), что для всех L_z0,v в объединении (3.5)

1) (x_x,Bⁱ(v))+(x_z,v) Ё e > 0,

2) L₀(xⁱ(z₀),z₀) Ё 1.

Тогда не более чем конечное число множеств W_k непусто.

Замечание Условия теоремы требуют, чтобы все лучи (xⁱ(L_z0,v),L_z0,v) принадлежали квадранту (части пространства, ограниченной двумя гиперплоскостями, не параллельными L₀(x,z) = 1), который лежит в положительном полупространстве относительно плоскости L₀(x,z) = 1. q.e.d.

Доказательство В условиях теоремы лучу (xⁱ(L_z0,v),L_z0,v) сопоставляется луч L_{[(z)\tilde]0,[(v)\tilde]} по правилу

~ z   0  = X(z0),  ~ v   = Ф Г Г Г Г Х ~ v   L  ~ v   R  Ж В В В В Ь = Ф Г Х (xx,Bi(v))+(xz,v) (cx,Bi(v))+(cz,v) Ж В Ь .

(3.6)

Из условия теоремы следует, что

~ v   L  = (xx,Bi(v))+(xz,v) Ё e > 0.

(3.7)

Из представления (3.5) получаем следующее представление для [(W)\tilde] = Xⁱ(W) ([(W)\tilde] л LR):

~ W   = х [(z)\tilde]0, [(v)\tilde]  L[(z)\tilde]0,[(v)\tilde], ~ z   0  н Xi(Wz): || ~ z   0  || < ~ b   , ~ v   н ~ V   ( ~ z   0  ) 0 < g ё   Ф ж ( ~ v   L  )2+( ~ v   R  )2   ё d .

(3.8)

Ввиду (3.7) множество [(W)\tilde] включено в некоторый угол, который задается прямыми U₁(L) = (d/e)L+U₁₂ ё 0 и U₂(L) = -(d/e)L+U₂₂ Ё 0. Утверждение теоремы следует из пункта 5) леммы 5 и леммы 6. q.e.d.

Теорема 5 Пусть существует такая вершина i, что для всех лучей L_z0,v в объединении (3.5)

1) (x_x,Bⁱ(v))+(x_z,v) = 0,

2) (c_x,Bⁱ(v))+(c_z,v) = 0.

Тогда не более чем конечное число множеств W_k непусты.

ДоказательствоИз условий теоремы вытекает, что множество [(W)\tilde] является ограниченным на плоскости LR: ввиду (3.6), [(W)\tilde] = Xⁱ(W) = Xⁱ(W^z). Утверждение теоремы следует из пункта 4) леммы 5 и леммы 6. q.e.d.

Теорема 6 Пусть выполнены условия 1) и 2) предыдущей теоремы. Если в дополнение к ним выполнено условие

3) для любого z₀ н W^z: L₀(xⁱ(z₀),z₀) = U₁, R₀(xⁱ(z₀),z₀) = U₂, где U₁ и U₂ - некоторые константы,

то не более чем одна из областей {W_k} непуста.

Доказательство Из условий теоремы следует, что вершина i отображается в точку (U₁,U₂)^T плоскости LR. Поскольку множества M_k не пересекаются, то точка (U₁,U₂)^T может попасть не более чем в одно из них. Воспользовавшись леммой 6, получаем справедливость утверждения теоремы. q.e.d.

Теорема 7 [принцип неподвижной точки пространства итераций]

Пусть выполнены следующие условия.

1) Хотя бы одна вершина M(A,b(z)) имеет фиксированные координаты, не зависящие от внешних параметров.

2) x_z = 0 и c_z = 0; это означает, что L₀ и R₀ зависят только от параметров объемлющих циклов и не зависят от внешних переменных.

Тогда не более чем одна из областей {W_k}_{k = -╔}^╔ непуста.

Доказательство Проверим выполнение условий теоремы 6. Обозначим координаты вершины через xⁱ. Поскольку вершина имеет координаты, не зависящие от внешних параметров, то Bⁱ = 0. Следовательно, для всех L_z0,v в объединении (3.5) (x_x,Bⁱ(v))+(x_z,v) = (x_x,0)+(0,v) = 0, и (c_x,Bⁱ(v))+(c_z,v) = (c_x,0)+(0,v) = 0. Поскольку L₀ и R₀ зависят только от параметров цикла, то для любого z₀ н W^z: L₀(xⁱ(z₀),z₀) = (x_x,xⁱ)+(x_z,z₀)+l₀ = (x_x,xⁱ)+l₀ = U₁ и R₀(xⁱ(z₀),z₀) = (c_x,xⁱ)+(c_z,z₀)+r₀ = (c_x,xⁱ)+r₀ = U₂. Следовательно, условия теоремы 6 выполнены и теорема 7 справедлива. q.e.d.

Замечательная особенность последней теоремы состоит в том, что ее условия можно легко проверить исходя сразу из текста программы, не обращаясь к довольно сложному построению леммы 1. Есть основания полагать, что условия теоремы 7 выполнены для подавляющего большинства реальных программ класса VD, обрабатывающих упакованный треугольный массив.

3.6  Согласование адресных обращений

После исследования всех адресных обращений необходимо их согласование. Мы затронем только две проблемы для иллюстрации возможного пути решения остальных.

1) Нахождение размера используемой части массива. Мы можем решать эту задачу, используя технику пункта 2.3 для нахождения максимума L_k(x,z).

2) Согласование с линейными формами. Пусть мы восстановили какое-то адресное обращение к массиву P с нелинейной g(x,z) = F(L(x,z),R(x,z)). Может возникнуть такая ситуация, что в другом адресном обращении к массиву P функция g₁(x,z) имеет стандартную линейную форму. Логично предположить, что g₁ имеет представление g₁ = F(a,R₁), где a Ё 1. Это один из случаев, упоминавшихся в классификации пункта 3.2. В этой ситуации справедливы все теоремы пункта 3.5 с L₀ = 1, R₀ = g₁.

4   Пример

Было бы неинтересно применять идеи статьи к тривиальной подпрограмме S2 на рисунке 1. Поэтому разберем преобразование адресных обращений у реальной небольшой программы, хотя все наши результаты применимы к большим сложным программам со сложными циклическими конструкциями. Рассмотрим подпрограмму DPPFA из пакета LINPACK. Подпрограмма DPPFA методом квадратного корня (Холецкого) находит LU-разложение самосопряженной положительно определенной матрицы, причем матрица хранится в упакованном треугольном массиве. После подстановки индексных функций вместо индуктивных переменных (см. введение) мы получаем 7 нелинейных адресных обращений к массиву AP. Исследуем их в порядке следования по программе.

1. F = J(J-1)/2+K, K н [`(1,J-1)], J н [`2,N], W = {[`(2,╔)]}. L<sub>0</sub> = J, R<sub>0</sub> = K. У многогранника ограничений есть фиксированная вершина (1,2), индексы L<sub>0</sub> и R<sub>0</sub> не зависят от внешних параметров. Из теоремы 5 следует, что можно предъявить не более одной непустой области W<sub>k</sub>. K<sup>min</sup> = 1, (J-K)<sup>min</sup> = 1 (при J = 2, K = 1), W<sub>0</sub> = W = {[`(2,╔)]}, следовательно, исходные индексы L = J и R = K.

2. F = K(K-1)/2+1, K н [`(1,J-1)], J н [`2,N], W = {[`(2,╔)]}. L<sub>0</sub> = K, R<sub>0</sub> = 1. W<sub>0</sub> = W = {[`(2,╔)]}, исходные индексы: L = K и R = 1.

3. F = J(J-1)/2+1. Аналогично предыдущему: L = J, R = 1, W₀ = W.

4. F = K(K-1)/2+K, K н [`(1,J-1)], J н [`2,N], W = {[`(2,╔)]}. L₀ = K, R₀ = K. Результат: L = K, R = K, W₀ = W.

5. F = J(J-1)/2+K. Все дословно совпадает с шагом 1.

6. F = J(J-1)/2+J. J н [`1,N], W = {[`(1,╔)]}. L₀ = J, R₀ = J. W₀ = W = {[`(1,╔)]}, исходные индексы: L = J и R = J.

7. F = J(J-1)/2+J. Совпадает с шагом 6.

Теперь можно воспользоваться методом, предложенным во введении, для того, чтобы свести фрагмент к линейному классу.

5  Заключение

Была представлена техника, которая может быть использована для расширения традиционных рамок статического анализа программ. В несколько видоизмененном виде ее можно применять к программам, неявно работающим со стандартными многомерными массивами, что позволит применить статический анализ к программам на языке Си, которые используют изменяющиеся указатели.

Автор признателен Вл.В. Воеводину за постановку задачи, критику и внимание к работе. Совместные дискуссии с В.В. Воеводиным оказались весьма плодотворными и помогли придать результатам законченную форму. Несколько существенных замечаний сделал А.В. Фролов. Автор благодарен П.В. Харитонову за то, что он внимательно прочитал окончательный вариант и предложил ряд поправок.

Список литературы

[1]

Воеводин В.В. Математические основы параллельных вычислений. М.: Изд-во МГУ, 1991, 345 С.

[2]

Voevodin V.V. Mathematical foundations of parallel computing, Singapur: World Scient. Publ. Co., Ser. Computer Sc. 1992, Vol. 33, 343 P.

[3]

Voevodin V.V. Information structure of sequental programs // Russ. J. of Num. An. and Math. Modelling, 1995, Vol.10, N⁰3, P.279-286.

[4]

Воеводин Вл.В. Теория и практика исследования параллелизма последовательных программ//Программирование. 1992. N⁰3. С. 38-53.

[5]

Pugh W. A Practical Algorithm for Exact Array Dependence Analysis// Communs ACM. 1992. V.35.N⁰8. P.102-114.

[6]

Ашманов С.А., Тимохов А.В. Теория оптимизации в задачах и упражнениях. M.: Наука. Физматгиз, 1991.

[7]

Мину М. Математическое программирование. М.: Наука, Физматгиз, 1990, 488 С.
Minoux M. Paris: Programmation Matématique. Bordas et C.N.E.T-E.N.S.T., 1989.

[8]

Ковалев М.М. Дискретная оптимизация. Минск: Изд-во БГУ, 1977.

[9]

Гофман А.Дж., Краскал Дж.Б. Целочисленные граничные точки выпуклых многогранников.//Линейные неравенства и смежные вопросы. М.: Изд-во иностр. лит., 1959, С. 325-347.

[10]

Корбут А. А., Финкельштейн Ю.Ю. Дискретное программирование. M.: Наука, 1969.

[11]

Хеллер И., Томпкинс Ч.Б. Обобщение одной теоремы Данцига.//Линейные неравенства и смежные вопросы. М.: Изд-во иностр. лит., 1959, С. 348-351.

[12]

Кнут Д. Искусство программирования для ЭВМ. Т.1. Основные алгоритмы, M.: Мир, 1976.

• Перевод названия на английский язык:
  ``Applying linear index expressions reconstruction for reducing programs to the linear class.''

• Подпись автора: ............ /Д.В.Хмелёв/
• Дата отправки статьи: 10 июня 1997 года.
• Должность: студент 4 курса м/м МГУ им. М.В.Ломоносова, кафедра теории вероятностей.
• Домашний адрес: 117234, Воробьевы горы, ГЗ МГУ, Б-841.
• E-mail: dima@vvv.srcc.msu.su.

---

Last modified Fri May 24 19:43:05 BST 2002